DETERMINAN MATRIKS

DETERMINAN MATRIKS

Fungsi determinan matrik bujur sangkar A dinyatakan dengan det(A)=|A|, didefinisikan sebagai jumlahan hasil kali elementer elemen-elemen bertanda A.

Jenis-jenis Matriks

1. Derteminan n =1

     A=[a], det(A) =|a| = a

2. Determinan Matriks  n=2 (Ordo 2 x 2)

Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.

  

Nilai determinan A disimbolkan dengan , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.

  

Contoh:

Tentukan nilai determinan matriks

  

Pembahasan:

  

 3. Determinan Matriks n=3 (Ordo 3 x 3) Metode Aturan Sarrus

Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.

  

Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

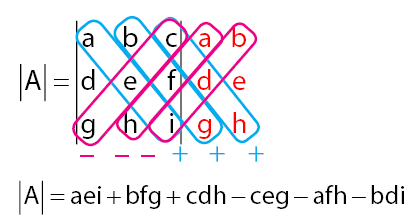
Contoh:

Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

Pembahasan:

Jawaban untuk matriks ordo 3 x 3 di atas ialah seperti berikut ini :

det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0  ) – ( 4 . 4 . 7  ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 ) 
               =      ( 8 )       +    ( 63 )     +       ( 0 )       –     ( 112 )     –      ( 0 )       –     15
               = – 56

Jadi, nilai determinan dari matriks ordo 3 x 3 di atas ialah = – 56.

*Metode Ekspansi Laplace

Andaikan, A=[aij] (nxn) adalah matrik bujur sangkar berordo (nxn).

(1). Minor elemen matrik A baris ke-i dan kolom ke-j (a-ij) ditulis Mij didefinisikan sebagai determinan matrik berordo (n-1)x(n-1) yang diperoleh dari A dengan cara menghilangkan baris ke-I dan kolom ke-j

(2). Kofaktor elemen matrik A baris ke-i kolom ke-j ditulis C-ij didefinisikan sebagai :

  

            

4. Determinan Metode Ekspansi Laplace

Andaikan, A=[aij] (nxn) adalah matrik bujur sangkar berordo (nxn), dan Cij = (-1)i+j Mij adalah kofaktor elemen matrik A baris ke-i kolom ke-j.

Contoh:

   

  

MATRIKS DAN JENIS-JENIS MATRIKS

MATRIKS

Apa itu Matriks?
= Matriks adalah susunan bilangan real, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun berbentuk empat persegi panjang yang dibatasi oleh tanda kurung.
Contoh Matriks:

Jenis-jenis Matriks

1. Matriks Baris dan Matriks Kolom
= Matriks baris adalah suatu matriks yang hanya memiliki satu baris aja. Matriks kolom adalah suatu matriks yang hanya memilki satu kolom saja.

Contoh:
   A = ( 2  9 ) atau B = ( 0  6  0  5 ) ...................................... Matriks Baris

...................................................... Matriks Kolom

2. Matriks Persegi/Bujur Sangkar
= Matriks yang memiliki jumlah kolom dan baris yang sama. Matriks persegi memilki ordo (nxn).

Contoh:

3. Matriks Segitiga Atas
= Matriks persegi dimana semua elemen dibawah diagonal utama bernilai 0.

Contoh:

4. Matriks Segitiga Bawah
= Matriks persegi dimana seua elemen diatas diagonal utama bernilai 0.

Contoh:

5. Matriks Diagonal = D
= Matriks persegi dimana semua elemen selain diagonal utama bernilai 0, dan elemen diagonal utama tidak bernilai 0.

Contoh:

6. Matriks Identitas = I
= Matriks  persegi dimana semua elemen selain diagonal utama bernilai 0, dan elemen diagonal utama bernilai 1.

Contoh:

7. Matriks Skalar
= Matriks persegi dimana semua elemen selain diagonal utama bernilai 0, dan elemen diagonal utama bernilai bukan 0 dan 1.

Contoh:

8. Transpose Matriks 
= Perubahan kolom menjadi baris. Bila Matriks A berukuran (mxn), Transpose Matriks A berukuran (nxm).

Contoh:

9. Matriks Simetris
= Matriks persegi dimana , Matriks A sama dengan Transpose Matriks A.

Contoh: 

Operasi Hitung pada Matriks

1. Penjumlahan

Operasi Penjumlahan

2. Pengurangan Matriks
= Sama seperti operasi hitung pada penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama.

Operasi Pengurangan

3. Perkalian Matriks
= Syarat dua buah matriks dapat dikalikan jika memilki jumlah kolom matriks A (pertama) sama dengan jumlah baris matriks B (kedua). Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom kedua.

Operasi Perkalian