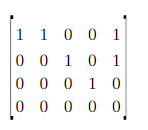BASIS DAN DIMENSI

BASIS dan DIMENSI

Basis

Andaikan V adalah sembarang ruang vektor dan S = {u1, u2,…,un} adalah himpunan berhingga vektor-vektor pada V, S dikatakan basis untuk ruang V jika :

§ S bebas linier

§ S membangun V

Dimensi

Sebuah ruang vektor dikatakan berdimensi berhingga, jika ruang vektor  V mengandung sebuah himpunan berhingga vektor S = {u1, u2,…,un} yang membentuk basis. Dimensi sebuah ruang vektor V yang berdimensi berhingga didefinisikan sebagai banyaknya vektor pada basis V.

Ruang Hasil Kali Dalam

Sebuah hasil kali dalam (inner product) pada ruang vektor riil V adalah fungsi yang mengasosiasikan bilangan riil [u,v] dengan masing-masing pasangan vektor u dan v pada V sedemikian rupa sehingga aksioma-aksioma berikut ini :

§ [u,v] = [v,u]    (aksioma simetri)

§ [u+v,w] = [u,w] + [v,w]    (aksioma penambahan)

§ [ku,v] = k[u,v]    (aksioma kehomogenan)

§ [u,u] ≥ 0 dan [u,u] = 0 Û u=0   (aksioma kepositifan)

Contoh :

Jika u = [u1,u2,…,un], dan v = [v1,v2,…,vn] adalah vektor-vektor pada Rn, maka :

                  [u,v] = u•v = u1v1 + u2v2 + … + unvn

adalah hasil kali dalam pada ruang Euclides Rn. Dan u dan v dikatakan ortogonal jika [u,v] = 0. Jika u ortogonal terhadap setiap vektor pada V, maka u dikatakan ortogonal terhadap V.

Basis Ortonormal

Sebuah himpunan vektor pada ruang hasil kali dalam dikatakan ortogonal jika semua pasangan vektor-vektor yang berada dalam himpunan tersebut ortogonal. Sebuah himpunan ortogonal yang setiap vektornya panjangnya 1 disebut ortonormal.

Contoh :

S={u1,u2,u3} dengan u1=[1,2,1], u2=[1,-1,1], dan u3=[1,0,-1]. Himpunan S adalah ortogonal pada R3, karena [u1,u2]=[u1,u3]=[u2,u3]=0

Catatan:

§Jika S = {u1, u2,…,un} adalah adalah basis ortonormal untuk sebuah ruang hasil kali dalam V, dan jika x sembarang vektor di V, maka :

                x = [x,u1]u1  + [x,u2]u2 +  … + [x,un]un  

§Misalkan V ruang hasil kali dalam dan {u1,u2,…,un} himpunan ortonormal Jika W ruang yang dibangun oleh u1,u2,…,un maka setiap vektor x dalam V dapat dinyatakan dengan : x = v + w dimana :

            v = [v,u1]u1  + [v,u2]u2 +  … + [v,un]un   

istilah ortogonal sebenarnya mempertegas bahwa proyeksi yang dilakukan haruslah membentuk hubungan tegak lurus antara ujung vektor yang diproyeksikan dengan ujung vektor hasil proyeksi.

Perubahan Basis

Misalkan S={u1,u2,…,un} basis lama ruang vektor V, dan B={v1,v2,…,vn} basis baru untuk ruang vektor V. Misalkan pula [x]S matrik koordinat x relatif terhadap S dan [x]B matrik koordinat x relatif terhadap basis B. 

RUANG VEKTOR, KOMBINASI LINIER, DAN KEBEBASAN LINIER

RUANG VEKTOR, KOMBINASI LINIER, DAN KEBEBASAN LINIER

RUANG –N EUCLIDES

Ruang-n Euclides

Jika n sebuah bilangan bulat positif, maka n-pasangan bilangan berurut adalah sebuah urutan n bilangan real (x1,x2,…,xn). Himpunan semua n-pasangan bilangan berurut dinamakan ruang-n Eucides dan dinyatakan dengan Rn.

Definisi. Misalkan u=[u1,u2,…,un]; v=[v1,v 2,…,vn] vektor di Rn.

§ u = v jika hanya jika u1 = v1, u2 = v2,…, un = vn

§ u + v = [u1 + v1, u2 + v2,…, un + vn ]

§ ku = [ku1, ku2,…, kun]

§ u•v = u1v1 + u2v2 + … + unvn

§ |u| = (u•u)1/2 

Ruang Vektor

Misalkan V sembarang himpunan. V dikatakan sebagai ruang vektor, bilamana aksioma-aksioma berikut dipenuhi :

(1) Jika u dan v vektor-vektor di V, maka u + v juga berada di V.

(2) u+v = v+u 

(3) u+(v+w) = (u+v)+w

(4) Ada sebuah vektor 0 di V sehingga 0+u=u+0

(5) Untuk setiap u di V terdapat  –u di V sehingga u+(-u) = -u+u =0

(6) Jika k skalar dan u di V, maka ku berada di V

(7) k(u+v) = ku + kv

(8) (k + l)u = ku + lu

(9) k(lu) = (kl)u

(10) 1u = u

Membangun Ruang Vektor

Jika u1, u2,…,un adalah vektor-vektor pda ruang vektor V, dan jika setiap vektor x pada V dapat dinyatakan sebagai kombinasi linier u1, u2,…,un, maka u1, u2,…,un dikatakan membangun ruang vektor V

1. KOMBINASI LINEAR

Definisi

Vektor V dikatakan merupakan kombinasi linier dari vektor – vektor v₁, v₂,…,v_n bila w bisa dinyatakan sebagai :

                                w = k₁v₁ + k₂v₂ + … + k_nv_n , dengan k₁,k₂,…,k_n adalah skalar.

TEOREMA

Himpunan semua kombinasi linear dari sembarang himpunan vektor-vektor yang tidak kosong dari V adalah suatu ruang bagian dari V

CONTOH SOAL KOMBINASI LINEAR

Diketahui a = (1, 2), b = (-2, -3), dan c = (1, 3). Apakah c merupakan kombinasi linear dari a dan b?

Jawab:

Misalkan c merupakan kombinasi linear dari a dan b maka dapat ditentukan dengan c = k₁a + k₂b

(1, 3) = k₁(1, 2) + k₂(-2, -3)

(1, 3) = (1k₁, 2k₁) + (-2k₂, -3k₂)

Maka dapat dinyatakan 1 = k₁ – 2k₂ dan 3 = 2k₁ – 3k₂ Sehingga diperoleh pengenyelesaian k₁ = 3 dan k₂ = 1

Jadi c merupakan kombinasi linear dari a dan b, dan dinyatakan dengan c = 3a + b

2. MEMBANGUN (MERENTANG)

Definisi

Himpunan vektor S = {s₁, s₂, ... , s_n} dimana s₁, s₂, ... , s_n Î V disebut membangun jika setiap v Î V, v  merupakan kombinasi linear dari S ,yaitu : v = k₁s₁ + k₂s₂ +…+ k_ns_n, dengan k₁,k₂,…,k_n adalah skalar.

CONTOH SOAL MEMBANGUN

      Vektor-vektor i=(1,0,0), j=(0,1,0), k=(0,0,1) merentang R³.

Jawab :

Misal x = (x₁, x₂, x₃) Є R³ sehingga akan dibuktikan k₁i + k₂j + k₃k = x

Jadi semua vector di R³ dapat dinyatakan sebagai kombinasi linear i, j, k; sehingga i, j, k membangun R³.

CONTOH LAIN

●      Polinom-polinom 1, x, x², ... , xⁿ membangun ruang vektor P_n, karena polinom p pada P_n dapat dituliskan sebagai        p = a₀ + a₁ x + a₂ x² +...+ a_n xⁿ

●      Yang merupakan kombinasi linear dari 1, x, x², ... , xⁿ  

3. BEBAS DAN BERGANTUNG LINEAR

Definisi

Jika S = {v₁, v₂, v₃, ……………,v_n}adalah himpunan vector sedemikian sehingga, k₁v₁ + k₂v₂ + … + k_nv_n = 0 maka S = {v₁, v₂, v₃,..., v_n} disebut :

1.       Bebas linier apabila scalar-skalar k₁, k₂,…,k_n semuanya nol.

2.       Bergantung linier apabila scalar-skalar k1, k2, k3,…, kn tidak semuanya nol.

CIRI-CIRI BEBAS DAN BERGANTUNG LINEAR

●        Himpunan vector S bebas linier jika system persamaan linier hanya mempunyai penyelesaian trivial (nol).

●        Himpunan vector S bergantung linier jika system persamaan linier mempunyai persamaan non trivial.

●        Vektor S merupakan bebas linear apabila

1.  Matrik tersebut det(S) ≠ 0.

2.  Ketiga vector tersebut mempunyai invers (sehingga dapat dibalik)

LATIHAN

1.       Misal u = (2, 4, 0), dan  v = (1,  –1, 3) adalah vektor-vektor di R³. Apakah vektor berikut merupakan kombinasi linear dari vektor – vektor di atas

a.       h = (4, 2, 6)

b.       j = (1, 5, 6)

c.        r = (0, 0, 0)

2.       Diketahui v =(3,9,-4,-2) merupakan kombinasi linier u₁= (1,-2,0,3), u₂ = (2,3,0,-1) dan u₃= (2,-1,2,1). Apakah v merupakan kombinasi linear dari u₁ , u₂ dan u₃ ?

3.       Apakah polinomial-polinomial berikut ini bebas linier ?        p₁ = 1 – 2x + 3 x² , p₂ = 5 + 6x – x² , p₃ = 3 + 2x + x²

JAWAB : 

1). Misal u = (2, 4, 0), dan  v = (1,  –1, 3) adalah vektor-vektor di R³.

    Apakah vektor berikut merupakan kombinasi linear dari vektor – vektor di atas
      a.       h = (4, 2, 6)
      b.       j = (1, 5, 6)
      c.        r = (0, 0, 0)
Jawab:

           ini juga dapat ditulis menjadi

          

          

    

2).  Diketahui v =(3,9,-4,-2) merupakan kombinasi linier u₁= (1,-2,0,3), u₂ = (2,3,0,-1) dan u₃= (2,-1,2,1). Apakah v merupakan kombinasi linear dari u₁ , u₂dan u₃ ?

Jawab: 

    Penyelesaiannya: x = 1, y = 3, dan z = -2

3). Apakah polinomial-polinomial berikut ini bebas linier ?       

p₁ = 1 – 2x + 3 x² , 

p₂ = 5 + 6x – x² , 

p₃ = 3 + 2x + x²

Jawab:

Untuk menguji polinomial bebas atau bergantung linier, langkah yang dilakukan adalah dengan menuliskan persamaan homogen sebagai berikut:

BASIS RUANG BARIS, BASIS RUANG KOLOM

BASIS RUANG BARIS, BASIS RUANG KOLOM

• DIMENSI 

Definisi:

Suatu ruang vektor tak nol V disebut berdimensi terhingga jika V berisi suatu himpunan vektor terhingga {v1,v2,…vn} yang membentuk suatu basis. Jika tak ada himpunan yang seperti itu, maka V disebut berdimensi tak hingga. Ruang vektor nol berdimensi terhingga

TEOREMA:

jika V adalah adalah suatu ruang vektor berdimensi terhingga dan {v1,v2,…vn} adalah sembarang basis, maka:

• Setiap himpunan dengan lebih dari n vektor adalah tak bebas secara linear
• Tidak ada himpunan dengan vektor yang kurang dari n yang merentang V.

TEOREMA:

•   Semua basis untuk suatu ruang vektor berdimensi terhingga mempunyai jumlah vektor yang sama
•   Suatu ruang vektor berdimensi terhingga V, yang dinyatakan dengan dim(V), didefinisikan sebagai jumlah vektor dalam suatu basis untuk V. Ruang vektor nol mempunyai dimensi nol.

Contoh

Menentukan basis dan dimensi ruang solusi dari SPL homogen

penyelesaian

Kita dapat menyatakan sistem ini dalam bentuk sebagai berikut

⇒  

⇒  

jadinya

membentuk ruang solusi SPL yaitu

yang menunjukkan bahwa vektor vektor merentang ruang solusi tersebut. Karena v1 dan v2 tidak saling berkelipatan satusama lain maka kedua vektor ini saling bebas bebas linear.Jadi (v1,v2) adalah basis bagi ruang solusi SPL yang dimaksud yang berdimensi 2.

 RUANG BARIS DAN RUANG KOLOM

• Jika A adalah  matriks mxn maka subruang yang direntang oleh vektor-vektor baris dari A disebut ruang baris dari A. Subruang dari yang direntang oleh vektor-vektor kolom dari A disebut ruang kolom dari A.

TEOREMA

• Jika suatu matriks U berada dalam bentuk baris eselon maka vektor-vektor baris dengan utama 1 (yaitu vektor-vektor tak-nol) membentuk suatu basis untuk ruang baris U dan vektor-vektor kolom dengan utama 1 dari vektor-vektor baris membentuk suatu basis untuk ruang kolom dari U.

misalkan matriks :

dengan melakukan OBE diperoleh

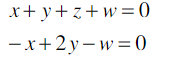
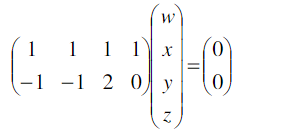
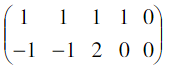
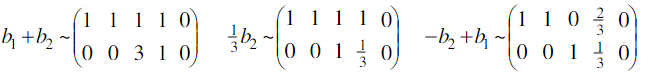
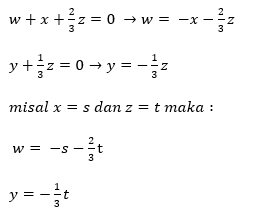
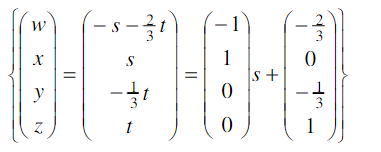
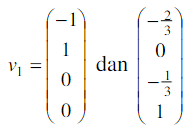
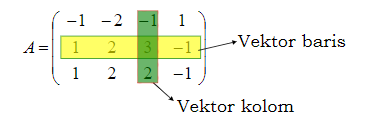
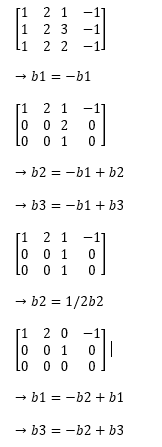
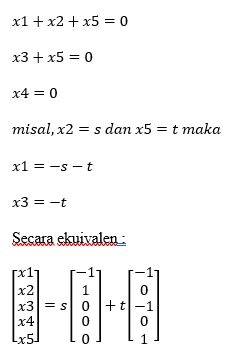
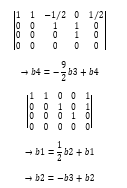
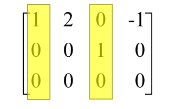→ perhatikan kolom-kolom pada matriks hasil OBE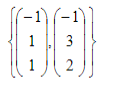

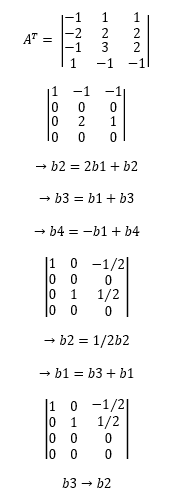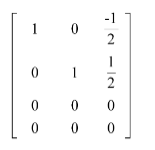
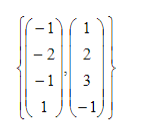
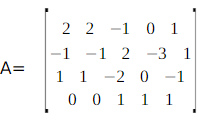
matriks A mempunyai basis ruang kolom yaitu :

basis ruang baris diperoleh dengan cara,Mentransposkan terlebih dahulu matriks A, lakukan OBE pada ,sehingga diperoleh :

⇒

Kolom-kolom pada matriks hasil OBE yang memiliki satu utama berseseuaian dengan matriks asal (A). Ini berarti, matriks A tersebut mempunyai basis ruang baris :

Defnisi RANK dan NULITAS

Dimensi dari ruang baris dan ruang kolom dari suatu matriks A  disebut rank dari A dan dinyatakan sebagai rank(A). Dimensi dari ruang nul dari A disebut sebagai nulitas dari A

dan dinyatakan sebagai nulitas(A).

Tentukan rank dan nulitas dari matriks berikut ini:

Penyelesaian:

dengan melakukan OBE diperoleh

⇒

karena terdapat 3 baris tak nol (atau secara ekuivalen, 3 satu utama),ruang baris dan ruang kolom keduanya berdimensi 3 sehingga rank dari (A)=3. Untuk menentukan nutulitas dari A,maka kita harus menentukan dimensi dari ruang solusi linier Ax=0. Sistem persamaan yang bersesuaian adalah

Kedua vektor tersebut membentuk basis untuk ruang solusi, sehingga nulitas(A) = 4.